

Generate a Fibonacci sequence where f(0)=1, f(1)=1
f(0)=1, f(1)=1, f(n)=f(n-1)+f(n-2)
a. construct the ratio of each pair adjacent terms in the fibonacci sequence. What happens as n increases? What about the ratio of every second term?
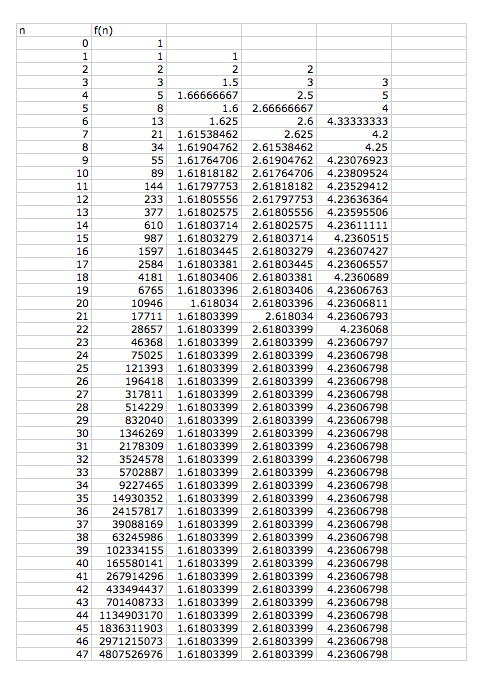
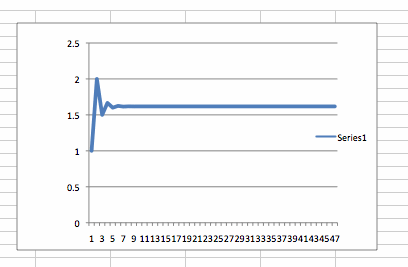
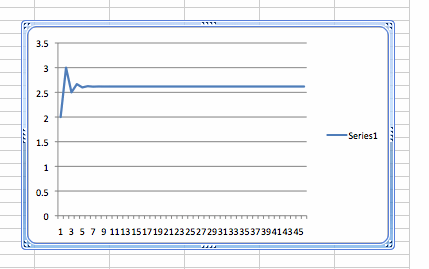
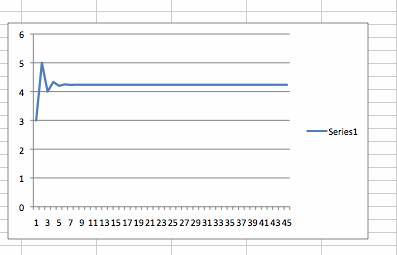
As shown above spreadsheet, we can notice that the ratio of each pair adjacent terms in the fibonnaci sequence is conveged.
It has converged to the number 1.61803399 which is golden ratio.
When we assumed that a(n)=f(n+1)/f(n) converges to L as n increases, we have
a(n)=f(n+1)/f(n)={f(n)+f(n-1)}/f(n)= 1+f(n-1)/f(n)= 1+[1/{f(n)/f(n-1)}]...
As n goes to infinity, L=1+1/L since f(n)/f(n-1) also converged to L
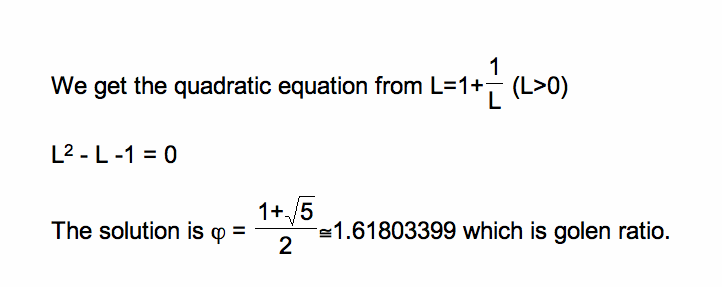
The ratio of every second term is converged 2.61803399 which is the square of golden ratio.
The ratio of every third term is converged to the number 4.23606798 which is the cube of golen ratio.
b. Explore sequences where f(0) and f(1) are some artirary integers other than 1. If f(0)=1 and f(1)=3, then your sequence is a Lucas Sequence. All such sequence, however, have the same limit of the ratio of successive terms.
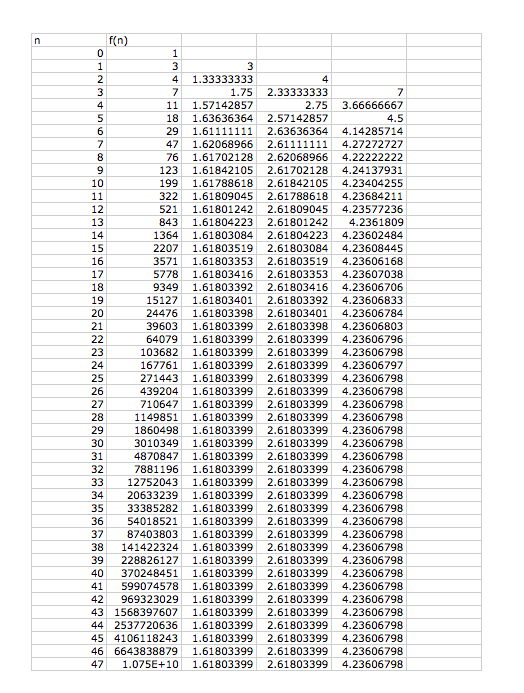
I started with f(0)=1, f(1)=3, then the sequence would be Lucan Sequence.
But, we can see the same result with previous fibonacci sequence.
That is, the ratio of each pair adjacent terms is still approaching to 1.61803399.
Also, the ratio of every second term and every third term are converged to 2.61803399 and 4.23606798 respectively.
I want to check other case where f(0)=3 , f(1)=7
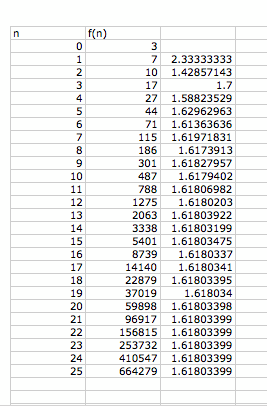
Observation : Suppose Lucas sequence where f(0) and f(1) are some artirary, then such sequences have the same limit of the ratio of successive terms.
Conclusion
The initial conditions of the Fibonacci Sequence does not affect the limit of the sequence of the ratio of successive terms of the Fibonacci Sequence.